We determine the area of the limiting shape by finding the area of each stage in the
construction, and finding the limit.
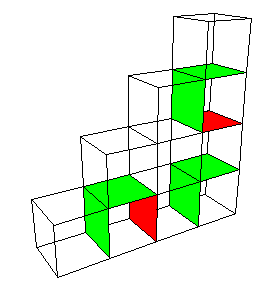
| Continuing in this way, the second stage of the construction consists of 27
cubes, each with side length 1/4. |
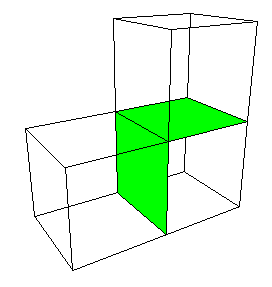
| Each cube has 6 faces, each of area (1/4)2. |
| So the area is |
A2 = 3*(3*(3*6*(1/4)2 - 4*(1/4)2)
- 4*(1/4)2) - 4*(1/4)2 |
= 6*33*(1/4)2 - 4*(1/4)2*(1 + 3 + 32) |
| Following this pattern, we see |
An = 6*3n+1*(1/4)n -
4*(1/4)n*(1 + 3 + 32 + ... + 3n) |
= 6*3n+1*(1/4)n - 4*(1/4)n*((1 - 3n+1)/(1 - 3)) |
|
| So An -> 0 as n -> infinity. |
| Consequently, the limiting shape has area 0, hardly a surprise because the
limiting shape is a gasket. |