| The dimensions of the cubes are divided by 1/2 at each
successive generation, so the thickness of the limiting shape is 0. |
| In fact, the limiting shape is a right isosceles Sierpinski gasket. |
| So it suffices to compute the perimeter of the gasket. |
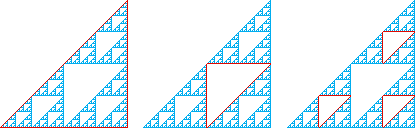 |
(left) The outer boundary, B0, of the gasket
has length 2 + sqrt(2). |
(center) The largest inner boundary, B1,
has length (2 + sqrt(2))/2. |
(right) The next largest inner boundaries, B2,
have lengths summing to 3(2 + sqrt(2))/4. |
| In general, Bn has lengths summing to
3n-1(2 + sqrt(2))/2n =
(3/2)n-1(2 + sqrt(2))/2. |
| So Bn -> infinity as n -> infinity, and
consequently the gasket has infinite perimeter. |