Block Fractals

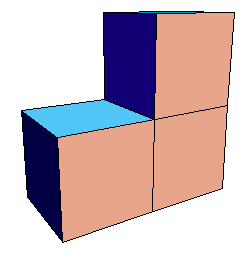
Suppose the cubes in the first picture have side length 1, hence volume 1. Then for this shape we see	V0 = 3*1
Then the cubes in the second picture have side length 1/2, hence volume (1/2)3 = 1/8. We see this shape has	V1 = 32*(1/8)
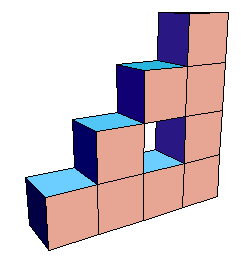
The cubes in the third picture have side length 1/4 = (1/2)2, hence volume ((1/2)2)3 = (1/8)2. We see this shape has	V2 = 33(1/8)2
In general,	Vn = 3n+1(1/8)n = 3*(3/8)n

So the limiting shape has volume 0. This is no surprise: the limiting shape is a right isosceles gasket.

Return to block fractal computations.