Block Fractals

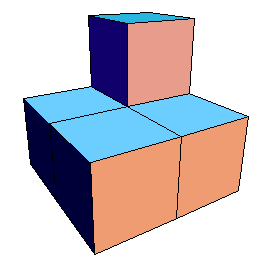
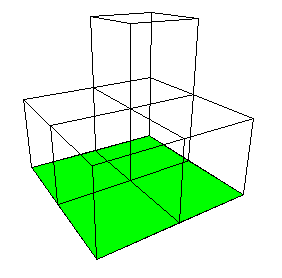
We show the area of the limiting shape is infinite by findinga sequence of squares in the limiting shape, and showing the sum of the areas of these squares diverges. Each stage of the construction contributes its own squares.

The initial stage consists of 5 cubes, each of side length 1.

The base has area = 4 and is part of all stages of the construction.

The first stage of the construction consists of 5 scaled copies of the initial stage.

The bases of four of these copies reconstitute the base of the initial stage.

The remaining copy contributes a new base, a square of area = 1.

Although part of this base overlaps with the top of one of the cubes of another copy, in the limiting shape that overlap reduces to a point. So in the limiting shape, this base is indeed part of the area of the shape.

The second stage consists of 25 scaled copies of the initial stage.

The bases of 16 of these copies reconstitute the base of the initial stage.

The bases of 4 of these copies reconstitute the base of the first stage.

The remaining 5 copies contribute 5 new bases, squares of area = 1/4.

Each of these bases is part of the surface of the limiting shape, so contributes to its area. The areas of the bases are

initial stage 4

first stage 1

second stage 5*(1/4)

third stage 5²*(1/4)² = (5/4)²

n^th stage (5/4)^n-1

So the area of these bases is infinite

Return to block fractal computations.