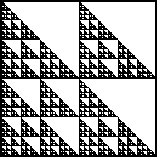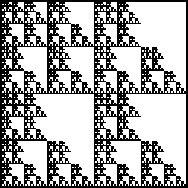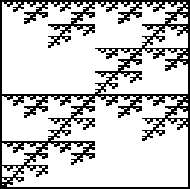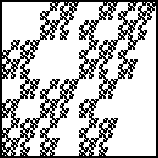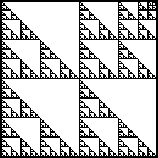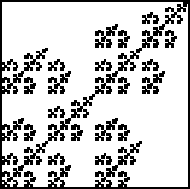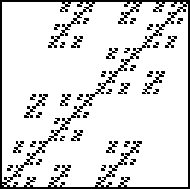| 1. Find IFS rules to generate these fractals.
Using a cm scale, measure the pieces to find the scaling factors.
Click each image for the solution. |
| (a) |
 |
|
(b) |
 |
| (c) |
 |
|
(d) |
 |
| (e) |
 |
|
(f) |
 |
| (g) |
 |
|
|
|
|
| |
| 2. Draw the graphs representing the allowed transitions for each of these
IFS with memory images. Click each image for the solution. |
| (a) |
 |
|
(b) |
 |
|
(c) |
 |
|
(d) |
 |
| (e) |
 |
|
(f) |
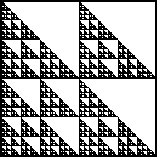 |
|
(g) |
 |
|
(h) |
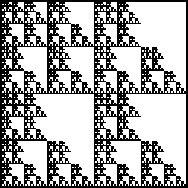 |
| (i) |
 |
|
(j) |
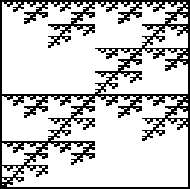 |
|
|
|
|
|
|
|
| |
| 3. Draw the graph representing the allowed transitions for each of these IFS with
memory images. Determine if each image can be generated by an IFS without memory.
For those than can be generated by an IFS without memory and with a finite set of
rules, write the IFS table. Click each image for the solution. |
|
| |
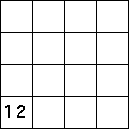
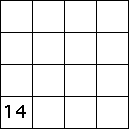
| 4. Suppose T1, T2, T3, and T4
are an IFS that generates the filled-in unit square. (The standard driven IFS
transformations are one example. In these problems we deal with other examples.) |
| In addition, suppose T2, T3, and T4 are
given in the table. |
| r | s | theta | phi | e | f |
| T1 | | | | | | |
| T2 | 0.5 | 0.5 | 0 | 0 | 0.5 | 0 |
| T3 | 0.5 | 0.5 | 0 | 0 | 0 | 0.5 |
| T4 | 0.5 | 0.5 | 0 | 0 | 0.5 | 0.5 |
|
| Fill in the parameters for T1 so the lower left corners have the indicated
addesses. Click each image for the solution. |
| (a) |
 |
|
(b) |
 |
|