Eighth Homework Set Answers

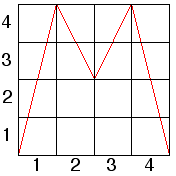
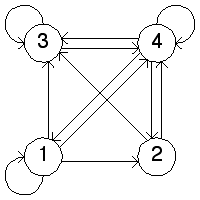
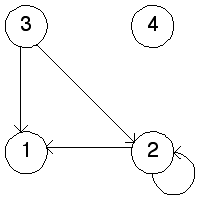
12. (a) On the right is the transition graph for the function on the left.

From the graph we see the forbidden transitions are 2 → 1, 2 → 2, 3 → 1, and 3 → 2. These are the arrows missing in the transition graph.

(b) Here is the fractal generated by this transition graph.

(c) The complementary transition graph is on the left, the attractor of the driven IFS is on the right.

Why does it look that way? The loop 2 → 2 generates the point with address 2∞, that is, the point with coordinates (1,0). The path 2 → 1 generates the point T1(1,0), that is the point wioth coordinates (1/2,0). No arrow goes to vertex 3, so nothing else is generated.

(d) The only obvious conclusion is that the IFS of a transition graph and its complement have complementary address length 2 squares occupied. That is, the empty squares of one are occupied squares of the other, and vice versa.

Return to Homework 8 Practice.