Eighth Homework Set Answers

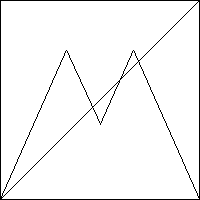
15. (a) Because xi+1 = T(xi) for all i, we see

xi+2 = T(xi+1) = T(T(xi)) = T2(xi)

Then (xi, xi+2) = (xi,T2(xi)). That is, every point of the second return map lies on the graph of T2.

(b) First,

A = T2(1/2) = T(T(1/2)) = T(3/4) = (3/2) - (3/2)(3/4) = 3/8

To find B < 1/2 with T(B) = 1/2, solve (3/2)B = 1/2, obtaining B = 1/3. (Recall for x ≤ 1/2, T(x) = (3/2)x. This is why T(B) = 1/2 becomes (3/2)B = 1/2.)

To find C > 1/2 with T(C) = 1/2, solve (3/2) - (3/2)C = 1/2, obtaining C = 2/3.

(c) We see the point (1/2, T2(1/2)) = (1/2, 3/8) lies on the graph of T2.

Next, T2(1/3) = T(T(1/3)) = T(1/2) = 3/4, so (1/3, 3/4) lies on the graph of T2. Similarly, (2/3, 3/4) lies on the graph of T2.

Finally, for 0 ≤ x ≤1/3, T(x) lies on the line between 0 and T(1/3) = 1/2, so T2(x) lies on the line between 0 and T2(1/3) = 3/4. Arguing similarly for 1/3 ≤ x ≤ 1/2, for 1/2 ≤ x ≤ 2/3, and for 2/3 ≤ x ≤ 1, we see the graph of T2 is

Return to Homework 8 Practice.