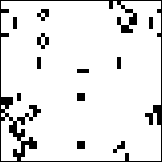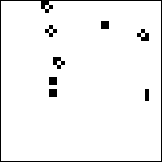| Not surprisingly, considerable effort has been exerted to try to understand
complex CA behavior. One promising, though still not universally
accepted, approach is Per Bak's notion of
self-organized criticality (SOC). |
| Many dynamical systems have stable and unstable fixed points. Only
the stable points are detected by iteration: any small departure from an unstable
fixed point iterates away from that point. |
| Nevertheless, as pointed out by Bak and others, some systems organize themselves into
critical configurations. Sandpiles are a good example. Falling sand forms a conical
heap. Adding more grains of sand causes avalanches, most small but some
extensive. The avalanches restructure the sandpile, returning it to its
critical shape. |
| The size of an avalanche is proportional to the reciprocal of the frequency of
avalanches of thaat size, hence the name 1/f scaling. |
| |
| Some have speculated that complex CA exhibit SOC. This can be tested by
starting a complex CA from a random initial distribution and letting it evolve until it
reaches a state with only constant or short-period repeating patterns: blocks, blinkers,
and the like. See the upper left image.
Here the CA is Conway's Life. |
| Next, perturn the state space by flipping the state of one cell. See the upper
right image, where the perturbation is in red. |
| Most perturbations die out quickly, but some persist for a considerable
time, the effects of this one cell boiling across the screen. See the lower
left image. |
| Eventually, the CA returns to a critical state. See the lower right image. |
 |
 |
| gen 467 | perturbation |
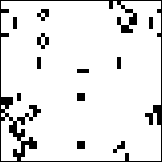 |
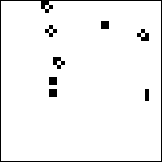 |
| gen 585 | gen 1005 |
|
| Some experiments have suggested that Life exhibits a 1/f distribution,
but so far delicate issues remain unresolved. |