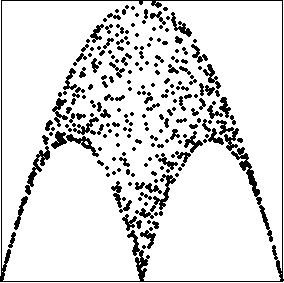
| To check the apparent synchronization suggested by the driven IFS, here we plot the
return maps for the average of two logistic maps. |
| Recall the return map for a single logistic map is just the
graph of the function y = L(x). So when the return map of the average of two coupled maps
is the graph of a logistic function, we have good evidence the functions have
synchronized. |
| Recall that we have simplified the general network to this |
| xn+1 | = (1 - c) ⋅ 4 ⋅ xn(1 - xn) +
c ⋅ 4 ⋅ yn(1 - yn) |
| yn+1 | = (1 - c) ⋅ 4 ⋅ yn(1 - yn) +
c ⋅ 4 ⋅ xn(1 - xn) |
|
| so c = 0 is the uncoupled system. |
| Note each is chaotic, exhibiting sensitivity to initial conditions, and we did
not start them at the same value, that is, x0 ≠ y0.
Nevertheless, they synchronize in a range
between about c = 0.3 and c = 0.7. |