| Here we couple logistic maps in a gasket pattern. This is part of Elena Malloy's project in the
summer of 2013. Individual maps are coupled in groups of 3. The
coupling strengths are |
| a couples each map to itself |
| b couples individual maps in groups of 3 to one another |
| c couples the averages of groups of 3 to themselves |
| d couples the averages of groups of 3 to one another |
| e couples the averages of groups of 9 to themselves |
| f couples the averages of groups of 9 to one another |
|
| Here the coupling constants must satisfy a + 2b + c + 2d + e + 2f = 1. |
 |
| With a = .01 b = .04, c = .01, d = .23, e = .14, and f = .15, here are the
return maps for x1 (far left), the average of x1, x2, and x3 (middle left),
the average of x1 through x9 (middle right), and the average of all 27 (far right). |
 
 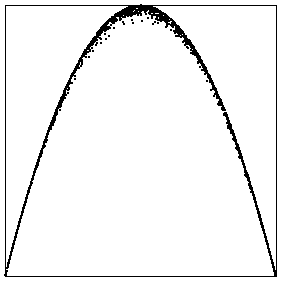 |
| The first three return maps look identical - really identical; time series reveal the differences of
corresponding values are under .001. So we find the peculiar situation that the groups of 9 have synvhronized, but
not to a simple logistic map. At the moment, we do not understand this system. |




