Circle Inversion Fractals

Properties of Inversion

Here we show that circles not passing through the center of the inverting circle invert to other circles not passing through the center of the inverting circle.

First we establish a property of circles:

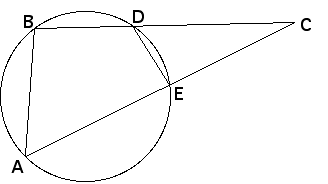
Given a point C outside the circle, suppose one line through C intersects the circle in points A and E, and another line intersects the circle in points B and D.

Then BC*DC = AC*EC, for all pairs of lines.

Here is a proof.

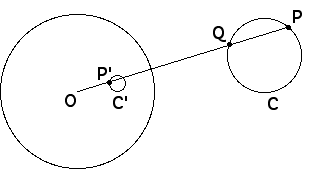
Now suppose C is a circle outside the inverting circle.

A point P on C inverts to a point P' with OP*OP' = r2, where r is the radius of the inverting circle. Consequently,

OP' = r2/OP

Let Q be the other point of C on the line through O and P.

Then by the result above, OQ*OP = k, so

OQ = k/OP

Combining the two red equations gives

OP'/OQ = r2/k

That is,

OP' = (r2/k)OQ

As Q traces out the points of C, P' also traces out a circle, because OP' is OQ, scaled by a constant factor r2/k.

An algebraic derivation of the formula for the center and radius of the inverted circle is found here.

Return to properties of inversion.