 |
 |
 | ||
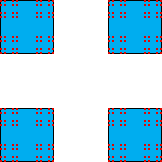
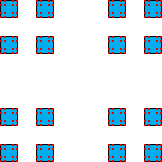
| N(1/3) = 2⋅2 | N(1/32) = 22⋅22 | N(1/33) = 23⋅23 |
| d | = limn→∞Log(N(1/3n)) / Log(1/(1/3n)) |
| = limn→∞Log(4n) / Log(3n) | |
| = Log(4) / Log(3) = 2⋅Log(2) / Log(3) |
| We select squares of side lengths | ||||||||||
| ||||||||||
| and in general | ||||||||||
| N(1/3n) = 2n⋅2n = 4n | ||||||||||
| Knowing N(1/3n) we can compute the box-counting dimension: | ||||||||||
|
Return to Dimension Algebra Exercises.