| We select cubes of side lengths 1/4, 1/16, ... , 1/4n, ...
noting the scaling of the Cantor middle-halves set. |
| Each square covering part of the gasket is the top face of cube covering part
of the product. |
| For cubes of side length 1/4n, each cube covering part of the top face gasket
is the top of a column of 2n cubes covering the product. |
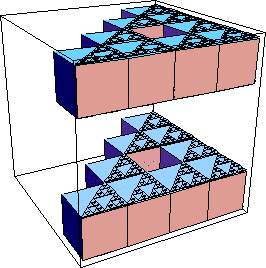 |
| Because we need 9n squares of side 1/4n to
cover the gasket, we need 9n⋅2n cubes of side length
1/4n to cover the product. That is, |
| N(1/4n) = 9n⋅2n |
| |
| Knowing N(1/4n) we can compute the box-counting dimension: |
| d | = limn→∞Log(N(1/4n)) / Log(1/(1/4n)) |
| = limn→∞Log(9n⋅2n) / Log(4n) |
| = limn→∞( Log(9n) / Log(4n) + Log(2n) / Log(4n) ) |
| = (Log(3) / Log(2)) + 1/2 |
|

