Dimensions of Projections

Projections of Fractal Graphs

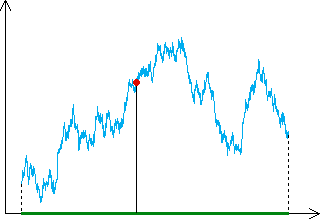
Here we see a graph of one-dimensional Brownian motion.

The term "one-dimensional" refers to the motion's being in one dimension, the y-axis in this case. The graph is a time record of vertical motion of a particle undergoing a random walk on the y-axis.

This graph is known to have dimension 3/2.

It projects to a line segment, of dimension 1.

Because it is a graph, any point of the line segment comes from a point of the graph.

In terms of dimensions we have 1 + 0 < 3/2, in contrast with the equality in the case of projecting Euclidean objects.

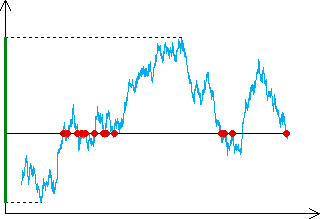
Note that the graph projects to a line segment on the y-axis, but most points on the line segment come from a complicated set of points, looking like a Cantor set. Could this be a Cantor set of dimension 1/2, reviving the conservation of dimension?

Return to projections.