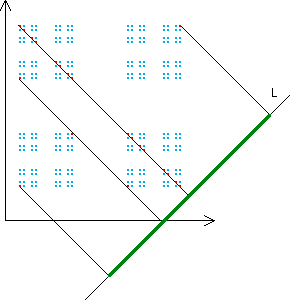
| To illustrate the range of results, we consider a simple example, the product of
two Cantor middle-thirds sets. |
| Each is made of N = 2 pieces scaled by r = 1/3,
so the dimension is Log(2)/Log(3). |
| Consequently, the product has dimension 2•Log(2)/Log(3). |
|
| On the left we project the product to the x-axis, obtaining a
Cantor middle thirds set. |
| A typical point in this Cantor middle thirds set comes from
a Cantor middle thirds set in the product.
In terms of dimensions, Log(2)/Log(3) + Log(2)/Log(3)
= 2•Log(2)/Log(3). |
| |
| On the right we project the product to the diagonal line, obtaining a
line segment. |
| Some points of this line segment come from isolated
points in the product, but most come from
Cantor sets in the product |
| The Cantor set indicated in the diagram is a Cantor middle-thirds
set, so in terms of dimensions we have |
| 1 + Log(2)/Log(3)
> 2•Log(2)/Log(3). |
|
|
|
|