Contractions

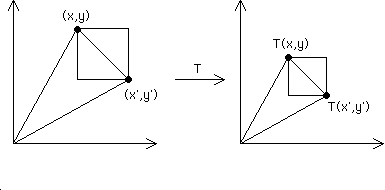
A contraction is a transformation T that reduces the distance between every pair of points.

That is, there is a number r < 1 with

dist(T(x, y), T(x', y')) ≤ r⋅dist((x, y), (x', y'))

for all pairs of points (x, y) and (x', y').

Here dist denotes the Euclidean distance between points:

dist((x, y), (x', y')) = ((x - x')2 + (y - y')2)1/2

To save space we write dist((x, y), (x', y')) = d((x, y), (x', y')).

The contraction factor of T is the smallest r satisfying

d(T(x, y), T(x', y')) ≤ r⋅d((x, y), (x', y'))

for all pairs of points (x, y), (x', y').

In general, contractions can reduce distances between points by different amounts, depending on the position of the points.

Here are some special kinds of contractions.

A similarity reduces all distances by the same number, r < 1. That is,

d(T(x, y), T(x', y')) = r⋅d((x, y), (x', y'))

for all pairs of points (x, y), (x', y').

The transformation T(x, y) = (r⋅x, r⋅y) is an example; its contraction factor is r.

An affinity reduces distances by different amounts in different directions. For example,

T(x, y) = (r⋅x, s⋅y),

where both r < 1 and s < 1, and r and s are different.

What is the contraction factor for the affinity T(x, y) = (x/2, y/3)? here is the Answer.

If all the transformations of an IFS are contractions, then iterating the IFS is guaranteed to converge to a unique shape.

Return to IFS Convergence.