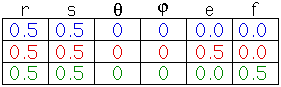
| Note that applying all three of these transformations to the gasket gives the
gasket again. |
| Click the gasket picture to see the
effect of applying these transformations to the gasket. |
|
| That is, the gasket is invariant under the
simultaneous application of these three transformations. |
| In fact, the gasket is the only (compact) shape left invariant. |
| What happens if we apply these transformations
to some shape other than the gasket? |
| What happens if we apply these transformations to the resulting shape? |
| What happens if
we iterate this process? Click the drawing for an animation,
or try your own drawing in the deterministic IFS software. |
| On the left is an instance of this idea applied to a sketch of my cat, on the right to a
sketch of my brother. Click each picture to see the process applied. Click the last picture in the sequence to
return to the first. |
|
| We observe a sequence of pictures that converges to the gasket, independently of the starting shape.
With a scanner and imagination,
some mischief can be achieved. |