Convergence of Deterministic IFS

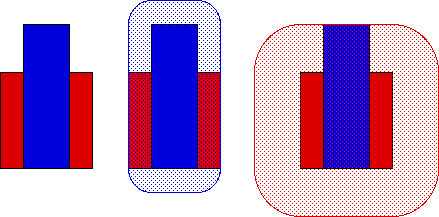
Suppose A and B are compact subsets of the plane. Then the Hausdorff distance between A and B is

h(A, B) = min{ε: A ⊆ Bε and B ⊆ Aε}.

For example, suppose A is the red unit square, and B is the rectangle with base length 1/2, height 3/2, and base centered along the base of the square.

What is h(A, B)?

We see

A is contained in B1/4 and

B is contained in A1/2.

These are the smallest ε-thickenings that will work:

for any ε < 1/4, Bε misses the left and right sides of A, and<

for any ε < 1/2, Aε misses the top of B.

So h(A, B) = 1/2. (Remember, the same ε must work for both A ⊆ Bε and B ⊆ Aε.)

As usual, the only work required in proving h is a metric lies in showing the triangle inequality holds. That is made easier by first proving the lemma

(Aε)δ ⊆ A(ε+δ).

Exercise Find h(A, B), where A is the union of the line segments from (0,1) to (0,0) and from (0,0) to (1,0), and B is the line segment from (0,1) to (1,0).

Return to Convergence of determinisitc IFS.