Convergence of Deterministic IFS

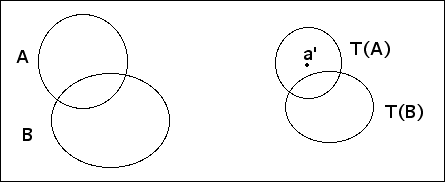
Now we relate the Euclidean contraction factor of

T:R2 → R2

to the Hausdorff contraction factor of

T:K(R2) → K(R2)

defined by T(A) = {T(x,y): for each (x,y) in A}.

Prop. 1 If T has Euclidean contraction factor r, then for all compact sets A and B in the plane

h(T(A),T(B)) ≤ r⋅h(A,B)

Proof Let h(A,B) = k. We want to show

T(A) ⊆ (T(B))r⋅k

and

T(B) ⊆ (T(A))r⋅k

That is, for every point a' of T(A) there is a point b' of T(B) with d(a',b') ≤ r⋅k.

For every point a' in T(A), there is some point a in A with T(a) = a'.

Return to Convergence of determinisitc IFS.