Spiral IFS

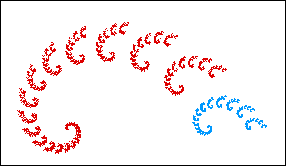
From our experience with the fern, we expect to decompose the spiral into a small number of pieces.

Indeed, two suffice:

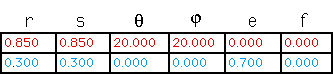
To determine scalings and angles, we use the method described in Measuring IFS Pieces.

Taking the segment ab as the horizontal base, the r scaling factor of the blue piece is cb/ab = 0.3.

The r scaling factor of the red piece is ad/ab = 0.85.

Analogous measurements give s = r for both pieces.

Taking the point a to be the origin, the red piece is rotated by the angle between ab and ad.

Finally, the horizontal translation of the blue piece is the length of ac.

Thus this spiral fractal is generated by these IFS rules.

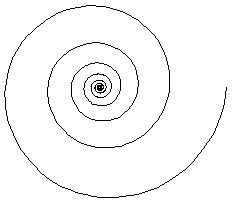
This spiral is a fractal, unlike the simple logarithmic spiral

which is not.

Here are some more examples.

Return to Natural Fractal Inverse Problems.