| First, note reflection across the x-axis equals reflection across
the y-axis followed by a 180 deg rotation. Consequently, both reflections can be achieved by
reflection across the y-axis. |
| The translations, e and f, are the same for the systems of equations and for the IFS parameters. |
| The remaining problem is this: given a, b, c, and d, find r, s, theta, and phi. |
| The first step of the conversion is this |
| a = r cos(theta) | b = -s sin(phi) |
| c = r sin(theta) | d = s cos(phi) |
|
| The magnitudes of r and s are easy to find. |
| a2 + c2 = r2cos2(theta) +
r2sin2(theta) = r2, | so r = sqrt(a2 + c2)
or r = -sqrt(a2 + c2) |
| b2 + d2 = s2cos2(phi) +
s2sin2(phi) = s2, | so s = sqrt(b2 + d2) |
|
| The sign of r is + if the transformation does not involve a reflection, - if it does. (Here
is how the initial and image points determine the presence of a reflection.) |
| Now to find the angles, |
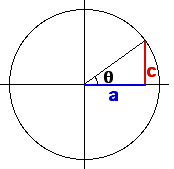 |
| a = r cos(theta) and |
| c = r sin(theta), so |
| c/a = (r sin(theta))/(s cos(theta)) |
| = tan(theta) |
|
 |
| b = -s sin(phi) and |
| d = s cos(phi), so |
| b/d = (-s sin(phi))/(s cos(phi)) |
| = -tan(phi) |
|
|
| So theta = arctan(c/a) and phi = arctan(-b/d), except arctan is single-valued only
between -90 and 90, but by taking
some care with the signs of a, b, c, and d, theta and phi can be extended to take values between -180 and 180. |
 |
| With these extra considerations, we have |
| r = (+/-)sqrt(a2 + c2) | s = sqrt(b2 + d2) |
theta = arctan(c/a) and | phi = arctan(-b/d) |
|
|



