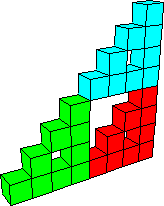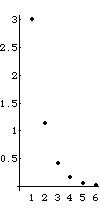Block Fractals

Sample - Volume

Here we compute the volumes of levels 1, 2, and 3, and the volume of the limiting shape.

Level 1	Level 2	Level 3

Level Side Length Number of Cubes Cube Volume Total Volume 1 1 3 1 V1 = 3*1 2 1/2 32 (1/2)3 = 1/8 V2 = 32*(1/8) 3 1/4 33 (1/4)3 = (1/8)2 V3 = 33*(1/8)2 ... ... ... ... ... n 1/2n-1 3n (1/2n-1)3 = (1/8)n-1 Vn = 3n*(1/8)n-1 = 3*(3/8)n-1
		Vol vs level

So the limiting shape has volume 0.

This is no surprise: the limiting shape is a right isosceles gasket, having dimension Log(3)/Log(2) < 3.

Volume is a 3-dimensional measure, so the volume of a Log(3)/Log(2)-dimensional object is 0.

Return to sample.