Complex Arithmetic

Background - Geometric

Complex numbers can be represented geometrically as points in the plane, taking the real part for the x-coordinate and the imaginary part for the y-coordinate.

1. Thinking of complex numbers as vectors in the plane, we see addition of complex numbers is just the familiar parallelogram law of vector addition.

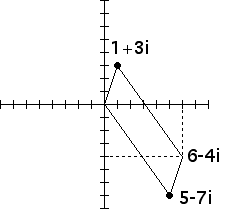2. At least from this point of view, multiplication does not have such a clear visualization.

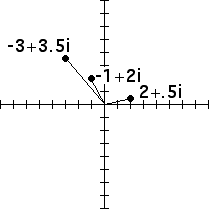The polar representation will reveal a simple interpretation.

3. The modulus sqrt(a² + b²) of the complex number a + bi is just the length of the corresponding vector.

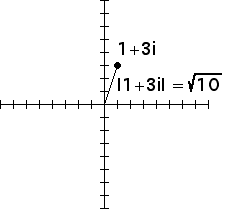Here are a few geometric problems in the sample.

Return to Background.