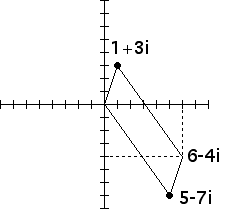
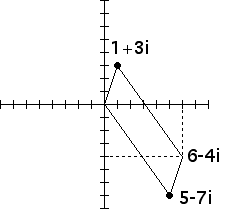
Purpose To develop some familiarity with the geometry of complex arithmetic.
Materials Graph paper, ruler, pencil, and calculator.
Conclusion Complex addition is easily understood by adding the real parts and adding the imaginary parts of the complex numbers. Complex multiplication is more easily understood in polar coordinates: the moduli are multiplied and the arguments are added. Using this interpretation of multiplication, we can get some idea of why the Mandelbrot set and Julia sets contain so many spirals.