Data Analysis by Driven IFS

Exercise Answers

6. (a)

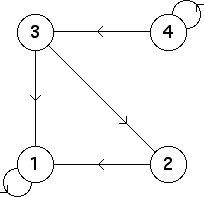
From the graph we see the allowed bin transitions are 1 -> 1, 2 -> 1, 3 -> 1, 3 -> 2, 4 -> 3, and 4 -> 4.

The occupied length 2 addresses are 11, 12, 13, 23, 34, and 44.

The empty length 2 addresses are the remaining ten 14, 21, 22, 24, 31, 32, 33, 41, 42, and 43.

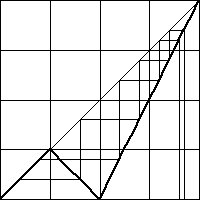
From the graph we see (1, 1) is a fixed point, as is every point on the segment from (0, 0) to (1/4, 1/4).

Except for iterations starting exactly at x = 1, all others will decrease for a few points, until they first reach a value <= 1/4, where they stop.

So unless we begin iteration at x = 1, the driven IFS will consist of a few points that soon end in a sequence converging to (0, 0).

Here is the transition graph.

The loop at 4 shows the driven IFS can generate the point with address 4infinity corresponding to the fixed point x = 1 we observed.

All other paths through the transition graph lead to 1, at which point we are forced to loop at 1.

So at least in this case, the behavior of the driven IFS can be read easily from the transition graph.

Return to Exercises.