Driven IFS and Financial Cartoons

Background

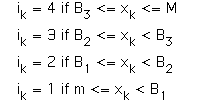
We use the four transformations

T1(x, y) = (x/2, y/2), the midpoint of (x, y) and (0, 0)

T2(x, y) = (x/2, y/2) + (1/2, 0), the midpoint of (x, y) and (1, 0)

T3(x, y) = (x/2, y/2) + (0, 1/2), the midpoint of (x, y) and (0, 1)

T4(x, y) = (x/2, y/2) + (1/2, 1/2), the midpoint of (x, y) and (1, 1)

Starting from a point (x0, y0) inside the unit square, standard iterated function system (IFS) theory shows the sequence (xk, yk) = Tik(xk-1, yk-1) uniformly fills up the unit square if the ik are independent and uniformly distributed in {1,2,3,4}.

To the extent that the square does not fill in uniformly, we can make deductions about the nonrandomness of the sequence {ik}.

Two issues remain:

how to interpret any departures from uniform fill of the square, and
how to convert a time series {x1, x2, ... , xn} into a symbol string {i1, i2, ... , in} of 1s, 2s, 3s, and 4s.

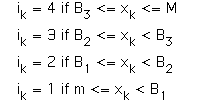Finally, we shall compare real financial data with the self-affine cartoons developed by Benoit Mandelbrot.

Return to Driven IFS and Financial Cartoons