



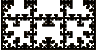
| 1-step memory | |
 |
Can we build pairs of lines whose endpoints belong to 2-cycles? One approach is to guess the placement of the lines and allow those pairs of transitions corresponding to occupied length 2 addresses. |
 |
What happens if we try to combine some of these lines? The results can be more complicated than we might expect. |
 |
Examining some of these combinations of lines leads to the notion of romes, central to understanding which of these pictures can be made by IFS without memory (but with more transformations). |
| 2-step memory | |
 |
Can we use 2-step memory to build 16 gaskets in the unit square? |
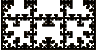 |
From the gaskets example, we see which 2-step memory configuration corresponds to
a given |
Return to IFS with Memory Lab.