Nonlinear Tessellations

Background

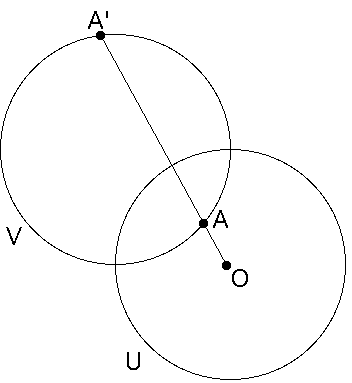
If circles U and V intersect orthogonally, the inverse in U of any point of V is another point of V.

Construction On the left we are given two orthogonal circles U and V and the point A lying within the circle U.

Draw a line through A and O, the center of U.

This line meets V at A', the inverse of A with respect to U.

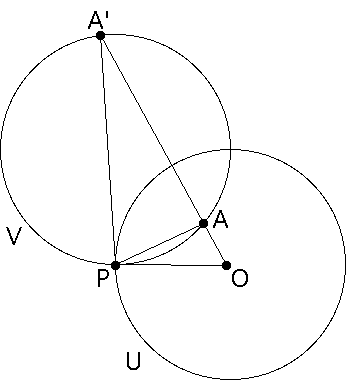Proof Draw segments OP, PA, and PA'.

We claim triangles OAP and OPA' are similar.

To see this, start by noting the angle at O is shared by both triangles.

The segment OP is a radius of U, hence is tangent to V at P.

The angles PA'A and APO intercept the same arc PA, and OP is tangent to V, so the angles PA'A and APO are equal.

Consequently, the triangles OAP and OPA' are similar.

As before, we see OA/OP = OP/OA'.

Cross-multiplying shows A and A' are inverses with respect to U.

That is, inversion in a circle U preserves all circles V that intersect U orthogonally. Of course, points of V that lie inside U are taken to points of V that lie outside U.

Return to Basic constructions.