Nonlinear Tessellations

Background

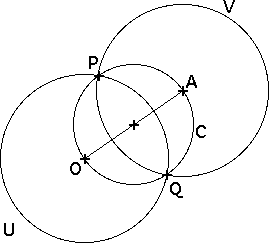
Constructing an orthogonal circle from an exterior point

Construction Draw the segment OA and the circle C with center the midpoint of segment OA and passing through O and A.

Denote by P and Q the points of intersection of C and U.

Then V is the circle with center A and passing through P.

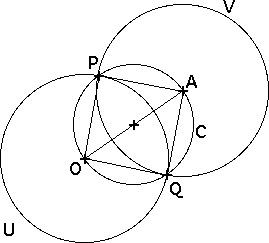Proof First show the segments PA and QA have the same length.

Note both angles OPA and OQA are inscribed in a semicircle of C, so both are right angles and consequently triangle OPA is congruent to triangle OQA.

So AP and AO have the same length and V passes through Q.

Because OP and OQ are radii of U and AP and AQ are radii of V, and the angles OPA and OQA are right angles, U and V are orthogonal at P and Q.

Return to Basic constructions.