| Next we add geodesics to produce more congruent hyperbolic triangles. |
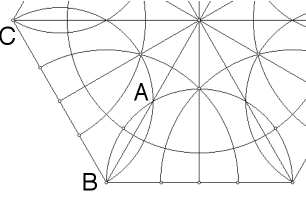
| We demonstrate this by adding geodesics through point A in the diagram
on the left. |
| These geodesics are rotations of the geodesic CAB about the
point A by angles of 30, 60, and 90. |
|
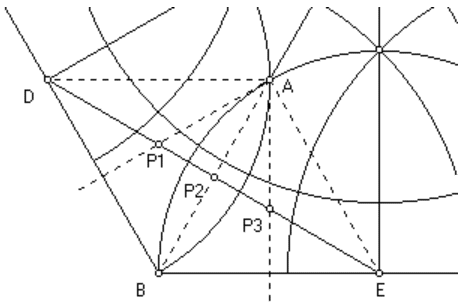
| Left: Geodesics are to be added through point A.
Right: Finding the poles P1, P2, and P3. |
| Because they are centers of geodesics through A, D and E lie on the
polar of A. |
| Thus each geodesic through A is an arc of a circle with
center on the line through D and E. |
| Rotate the segment AD about A by angles of 30, 60 and 90. |
| The intersection of these rotated segments with DE are the centers of
the circles determining the geodesics shown on the left. |
 |
| Left: Geodesics through A using P1, P2, and P3 as centers.
Right: The next level of tiles. |
| These new hperbolic triangles are congruent to one another, and to the
hyperbolic triangles constructed earlier. |
| Continuing this process can generate (many steps of) a tiling of the
Poincare disc. |