Nonlinear Tessellations

Background

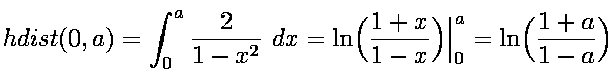
Sample calculation

More precisely, suppose the Poincare disc has center the origin and radius 1.

The formula for computing the hyperbolic distance along a geodesic is a line integral.

The integral becomes much simpler in the special case of calculating hyperbolic lengths along the x-axis.

The hyperbolic distance between the origin and the point (a,0) is

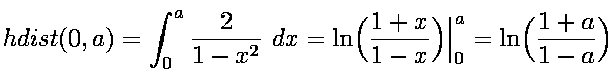First, it is easy to see that hdist(0,a) -> infinity as a -> 1, so an infinite hyperbolic extent is contained in a bounded Euclidean disc.

Second, to make the marks on the hyperbolic ruler above we began by noting

hdist(0,1/2) = ln((3/2)/(1/2)) = ln(3)

The second mark on the ruler is the number b satisfying

2*ln(3) = hdist(0,b), so 32 = (1+b)/(1-b) and b = (32-1)/(32+1) = 4/5.

In general, the nth mark of the ruler is at (3n - 1)/(3n + 1).

This is a quantitative expression of how hyperbolic distance appears to distort.

Return to yyperbolic distance and triangle congruency.