Nonlinear Tessellations

Background

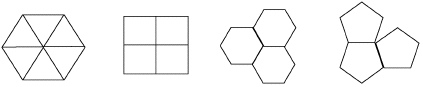
Perhaps the simplest tessellations of the plane are those of the regular polygons.

To tessellate (tile) the plane, the polygons must overlap only along their edges and completely fill the plane.

To tile the plane with congruent copies of a single regular polygon, the polygon must be an equilateral triangle, a square, or a regular hexagon.

In order to be able to tile the plane, the interior angle of a regular polygon must evenly divide 360. Certainly, this is true for these three polygons but not for the pentagon.

Here is a proof that no other regular polygons tile the plane.

Return to background.