Moments of a Continuous Distribution

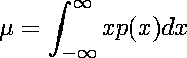
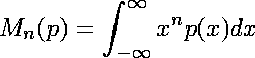
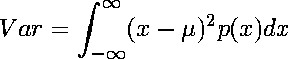
For a distribution taking on values x1, ..., xN, xi occurring with probability pi, we know the expected value, or average, is

x1p1 + x2p2 + ... + xNpN

Then for a continuous distribution p(x) the expected value, or mean, mu is

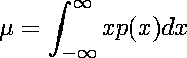In general, the nth moment of p(x) is

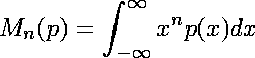So mu = M1(p).

The variance is the average value of (distance from the mean)2. That is,

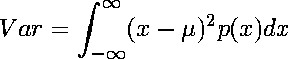Expanding (x - mu)2 and distributing the integrals, we see

Return to the standard deviation.