Pascal's Triangle and Its Relatives

Exercises

Other mods

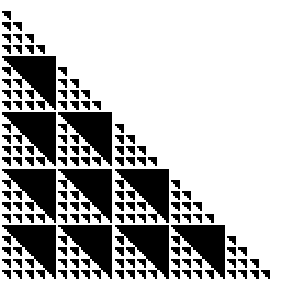
2. (mod 5) Shading the boxes of Pascal's triangle with numbers congruent to

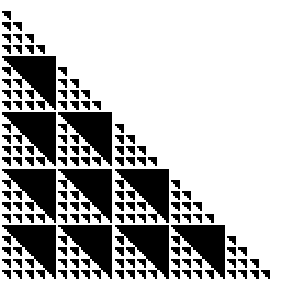0 (mod 5)	1 (mod 5)	2 (mod 5)	3 (mod 5)

4 (mod 5)	1, 2, 3, or 4 (mod 5)

Because 5 is prime, Z5 has no proper subgroups.

Consequently, there are no nontrivial cosets or quotient groups.

Return to Other Mod Exercises.