Pascal's Triangle and Its Relatives

Exercises

Symmetries of regular polygons

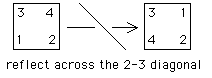
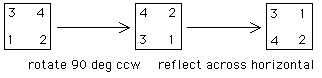
2. First, here is a reflection of the square across a diagonal.

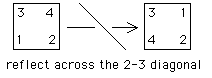Next, here is a 90 deg ccw rotation followed by reflection across the horizontal bisector of the square.

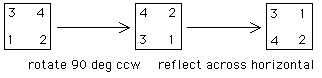So reflection across this diagonal is equivalent to rotating 90 deg ccw and then reflecting across the horizontal bisector of the square.

The symmetries of a regular polygon are reflections or rotations, because symmetries must take consecutive vertices to consecutive vertices.

The orientation-preserving symmetries are rotations.

The orientation-reversing symmetries are reflections.

Pick a reflection c and suppose d is any other reflection.

Then cd is orientation-preserving, so cd = r, a rotation, and

d = c2d = c(cd) = cr

because c2 = identity, for any reflection c.

Return to Symmetries of Regular Polygons Exercises.