|
| From our experience with spiral fractals, we
know these videofeedback pictures are not fractals. |
| Nevertheless, informed by this lab we can make a start at finding an IFS to generate this spiral. |
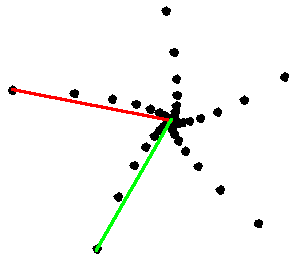
| Place the origin of the coordinates at the center of the spiral. |
| Measure the length of the segment from the origin to the most distant
point of the spiral. For this example we measure 4.5 cm. |
| Measure the length of the segment from the origin to the second-most distant
point of the spiral. For this example we measure 4.1 cm. |
| The ratio second length/first length gives the
scaling factor of one of the transformations. For this example we calculate r = s =
4.1/4.5 = .91. |
| The angle between the second segment and the
first segment gives the theta = phi value for this transformation.
For this example we measure theta = phi = 71 deg. |
| For this example we have |
| r | s | theta | phi |
e | f |
| 0.91 | 0.91 | 71 | 71 |
0 | 0 |
|
| The IFS consisting of this transformation alone generates a single point, the center of the spiral. |
| At least two choices of second transformation gives an IFS that generates the whole spiral. |
| r | s | theta | phi |
e | f |
| 0.91 | 0.91 | 71 | 71 |
0 | 0 |
| 0.0 | 0.0 | 0 | 0 |
1 | 0 |
|
| The second transformation must have r = s = 0, or else we will get a
sprial made of spirals. |
| This approach works well with the random IFS program.
|
| The other approach is to start with a point (or disc) at (1,0), or whatever point you prefer,
and take the second transformation to be the identity. |
| r | s | theta | phi |
e | f |
| 0.91 | 0.91 | 71 | 71 |
0 | 0 |
| 1.0 | 1.0 | 0 | 0 |
0 | 0 |
|
| This approach works well with the deterministic IFS program.
Take the starting shape to be a small disc. Under the Edit menu, select Animation. Set Generations to
auto-run to 40 and Pause length to 0.1. |
| By varying the IFS scaling (camera zoom) and rotation (camera angle), a variety of stable
spiral pattens can be produced. |
|
|
|
|
|
|