| From the form Nf(x) = x - (f(x)/f '(x)) we see that
roots of f(x) are fixed points of Nf(x): |
| |
If f(x*) = 0 and f'(x*) ≠ 0, then it is clear that
Nf(x*) = x*. |
Even if f '(x*) = 0, for fairly general functions f(x)
(any function represented by a Taylor series will work),
the function Nf(x) can be defined on x*, and for this extended function
Nf(x*) = x*. |
| Moreover, simple calculations show that each root of f(x) is a stable
fixed point for Nf(x). |
| |
| Finding the basins of attraction of the roots of f(x) is relatively
straightforward using graphical iteration of Nf(x). |
| This is most easily seen through an example. We take f(x) = (x+1)x(x-1),
a function whose roots are -1, 0, and 1. |
| On the left (a) we see the graph of Nf(x); the vertical dashed lines are
the points at which f '(x) = 0. |
| Certainly, we see that iteration from an initial point to the right of the right
vertical dashed line converges to x = 1, and iteration from an initial point to the left of
the left vertical dashed line converges to -1. Are these the entire basins of
attraction of +1 and -1? |
|
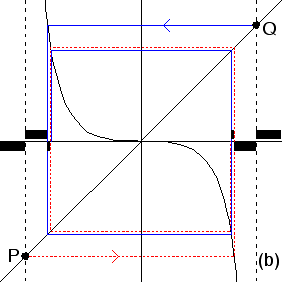
| The answer is "No." We can see this by reversing graphical iteration. |
| Denote by P and Q the intersections of these vertical dashed lines with the diagonal. |
| Now do reverse graphical iteration from P and Q. That is, go horizontally to the graph, vertically
to the diagonal. See the right picture (b). |
| This produces sequences of intervals converging to +1 (indicated by the bars above the
x-axis), and to -1 (bars below the x-axis). |
| Note these reverse graphical iteration paths appear to converge. In fact, they converge to a 2-cycle
for Nf(x). Iteration from points within the 2-cycle converges to x = 0. |