Julia Sets and the Mandelbrot Set

Real Newton's Method

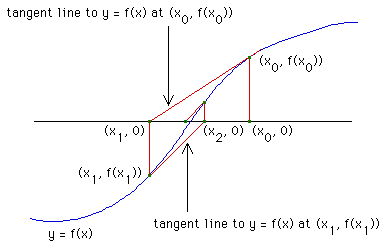
Newton devised an iterative process, called Newton's Method for finding the roots of functions.

A root of a function f(x) is a number x* for which f(x*) = 0. That is, the graph of y = f(x) crosses the x-axis at x*.

Here is Newton's method.

• Guess a number x₀ If f(x₀) = 0, we're finished. If not,
• Draw the vertical line from (x₀,0) to (x₀,f(x₀)).
• Draw the line tangent to the graph of y = f(x) at the point (x₀,f(x₀)).
• Usually, this tangent line intersects the x-axis at a point (x₁,0).
• Repeat the process with x₁ taking the place of x₀.
• Continue until f(x_i) is close enough to 0.

Click the picture to animate.

Being the inventor of calculus, Newton was able to find a compact expression for this construction.

x1 = x0 - f(x0)/f '(x0)

x2 = x1 - f(x1)/f '(x1)

...

Writing N_f(x) = x - f(x)/f '(x), Newton's method can be encapsulated in a single iterative scheme:

x_n+1 = N_f(x_n).

Return to real Newton's method.