Multifractals

Dimension of the Second-Highest Section

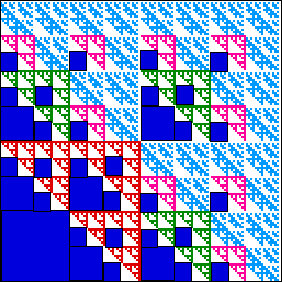
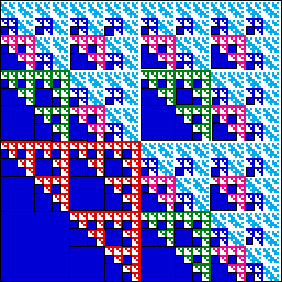
We count the empty squares that come from the gaskets.

There is one empty square of side 1/4, contributed by the gasket of side 1/2.	There are 6 empty squares of side 1/8: three from the gasket of side 1/2 and one from each of the three gaskets of side 1/4.
There are 27 empty squares of side 1/16: nine from the gasket of side 1/2, three from each of the three gaskets of side 1/4, and one from each of the nine gaskets of side 1/8.	There are 108 empty squares of side 1/32: 27 from the gasket of side 1/2, nine from each of the three gaskets of side 1/4, three from each of the nine gaskets of side 1/8, and one from each of the 27 gaskets of side 1/16.

Organizing the data into a table can reveal a pattern in the number of empty squares.

	square side 1/4	square side 1/8	square side 1/16	square side 1/32
gasket side 1/2	1*1	1*3	1*9	1*27
gasket side 1/4	0	3*1	3*3	3*9
gasket side 1/8	0	0	9*1	9*3
gasket side 1/16	0	0	0	27*1

So we see the number of empty squares fit into this pattern:

1		of side length 1/4 = 1/22
2*3		of side length 1/8 = 1/23
3*32		of side length 1/16 = 1/24
4*33		of side length 1/32 = 1/25
...
(n+1)*3n		of side length 1/2n+2

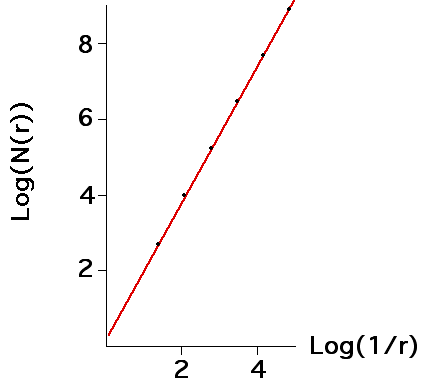
So the number N(r) of squares of side length r needed to cover the shape is

42 - 1		of side length 1/4 = 1/22
82 - 4*1 - 2*3		of side length 1/8 = 1/23
162 - 42 - 4*2*3 - 3*32		of side length 1/16 = 1/24
322 - 43 - 42*2*3 - 4*3*32 - 4*33		of side length 1/32 = 1/25
...
(2n+2)2 - 4n - 4n-1*2*3 - 4n-2*3*32 - ... - (n+1)*3n		of side length 1/2n+2

A plot of Log(N(r)) vs Log(1/r) shows the points fall along a straight line of slope about 1.75, so the set consisting of the second-highest boxes has dimension about 1.75.

Return to dimension calculation.