| The doubling map D:R → R is defined by |
| D(x) = 2x |
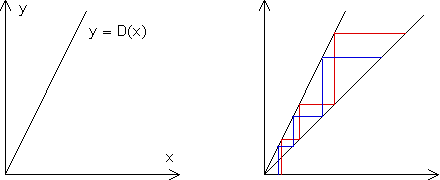
| On the left we see (part of) the graph of the doubling map; on the right is an illustration of sensitivity to initial conditions. Under graphical iteration, two nearby initial values (blue and red on the x-axis) iterate to values quite far apart on the diagonal. (In fact, the distance between the blue and red points doubles with each iteration.) This shows the doubling map exhibits sensitivity to initial conditions. |
 |
| On the other hand, except for the fixed point at the origin, the doubling map has no periodic points at all: |
| x = Dn(x) becomes x = 2nx. |
| For n ≠ 0 this is true only for x = 0. Consequently, although the doubling map exhibits sensitivity to initial conditions, it does not exhibit chaos. |
| That is, sensitivity to initial conditions (the butterfly effect) does not imply chaos. |