.gif)
.gif)
| The scaling condition is |
| (dt1)H - (dt2)H + (1 - dt1 - dt2)H = 1 |
| To simplify the notation, set |
| We want to show the function |
| f(x) = aH - xH + (1 - a - x)H |
| satisfies f(x) = 1 for exactly one value of x in the range |
| First, the graph of f(x) is decreasing because the derivative |
| f '(x) = -bxb-1 - (1 - a - x)b-1 |
| is negative. |
| To show f(x) = 1 has a unique solution, we must show
|
| Observe f(0) = aH + (1 - a)H. |
| Certainly, we must have
|
| First, taking |
 |
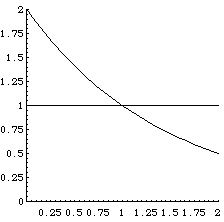
| Plot of |
| Proving |
| Instead, we establish the plausibility of this result by plotting |
| y = f(0) = aH + (1 - a)H. |
| Note |
.gif) |
| Finally, note |
.gif) |
| So given dt1 in the range |
Return to the Scaling Condition.