 split as
split as 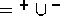 , with
, with
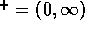 and
and  . On
. On 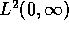 we introduce a
window function
we introduce a
window function  such that
such that 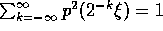 and
and  is supported in
is supported in  . We can clearly view
. We can clearly view  as a window function over the interval
as a window function over the interval 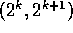 and observe that
and observe that
We consider the frequency line  split as
split as 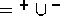 , with
, with
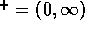 and
and  . On
. On 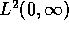 we introduce a
window function
we introduce a
window function  such that
such that 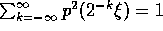 and
and  is supported in
is supported in  . We can clearly view
. We can clearly view  as a window function over the interval
as a window function over the interval 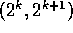 and observe that
and observe that
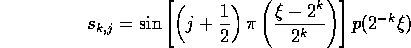
form an orthonormal basis of  . Similarly
. Similarly

gives another basis, whose elements are not orthogonal to those of the first
one. If we define  as an odd extension to
as an odd extension to  of
of 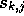 and
and
 as an even extension we find
as an even extension we find  permitting us
to write
permitting us
to write 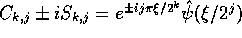 where
where
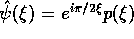 is the Fourier transform of the
wavelet
is the Fourier transform of the
wavelet  (cf. [4]).
(cf. [4]).
Thus, wavelet analysis corresponds to windowing frequency space in ``octave''
windows  .
.
A natural extension is provided by allowing all dyadic windows in frequency space and adapted window choice. This sort of analysis is equivalent to wavelet packet analysis.
The actual fast wavelet packet analysis algorithms (wavelets being a special cases) permit us to perform an adapted Fourier windowing directly in time domain by successive filtering of a function into different regions in frequency. The dual version of the window selection provides an adapted subband coding algorithm.
The wavelet packet library is constructed by iterating the wavelet algorithm. This library contains the wavelet basis, Walsh functions, and smooth versions of Walsh functions called wavelet packets (cf. [5])
These waveforms are mutually orthogonal. Moreover, each of them is orthogonal to all of its integer translates and dyadic rescaled versions. The full collection of these wavelet packets (including translates and rescaled versions) provides us with a library of ``templates'' or ``notes'' which are matched ``efficiently'' to signals for analysis and synthesis (cf. [2]), Wavelet packet expansions correspond algorithmically to subband coding schemes and are numerically as fast as the FFT.