Block Fractals

We determine the area of the limiting shape by finding the area of each stage in the construction, and finding the limit.

The initial stage consists of three cubes, each of side length 1.

Each cube has 6 faces, each of area 1.

Interior faces do not contribute to the surface area, and two pairs of cubes share two faces, making them interior.

So the area is

A0 = 3*6*1 - 4*1

The first stage of the construction consists of 9 cubes, each of side length 1/2.

Each cube has 6 faces, each of area 1/4.

This shape consists of three scaled copies of the initial shape, each with four interior faces.

In addition, the joining of these copies forms four interior faces.

So the area is

A1 = 3*(3*6*(1/4) - 4*(1/4)) - 4*(1/4)

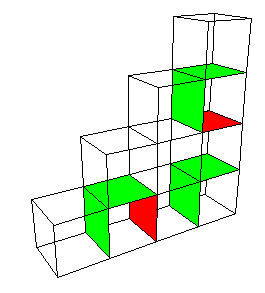
Continuing in this way, the second stage of the construction consists of 27 cubes, each with side length 1/4.

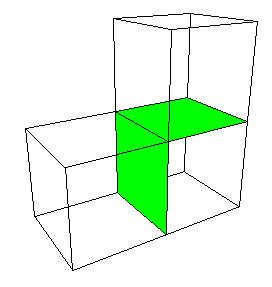
Each cube has 6 faces, each of area (1/4)2.

So the area is

A2 = 3*(3*(3*6*(1/4)2 - 4*(1/4)2) - 4*(1/4)2) - 4*(1/4)2

= 6*33*(1/4)2 - 4*(1/4)2*(1 + 3 + 32)

Following this pattern, we see

An = 6*3n+1*(1/4)n - 4*(1/4)n*(1 + 3 + 32 + ... + 3n)

= 6*3n+1*(1/4)n - 4*(1/4)n*((1 - 3n+1)/(1 - 3))

= 12*(3/4)n + 2*(1/4)n

So An -> 0 as n -> infinity.

Consequently, the limiting shape has area 0, hardly a surprise because the limiting shape is a gasket.

Return to block fractal computations.