Deterministic Chaos

6.G. Period-Doubling Bifurcations

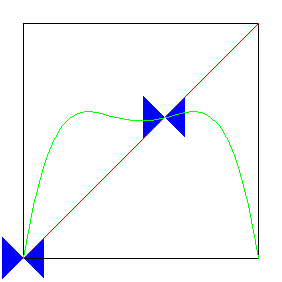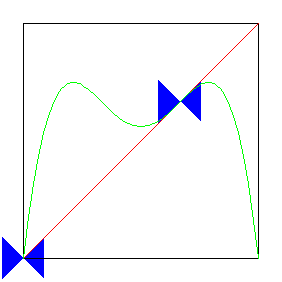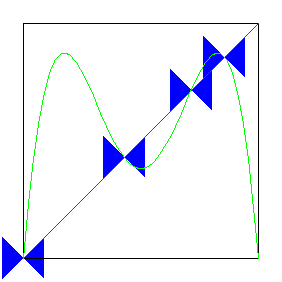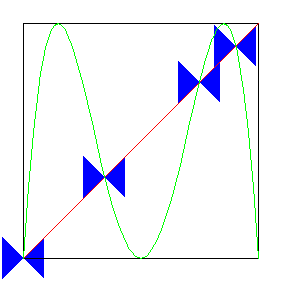
A period-doubling bifurcation occurs when

the graph of L(x) passes from inside the blue bowtie to outside, crossing over the diagonal line.

This introduces two new fixed points, both stable, at least before s increases very much.

For this 2-cycle, the original fixed point (a 1-cycle) becomes unstable at the same s-value that the 2-cycle appears. This is the source of the name period-doubling.

Click the animation to stop.

Return to Determinisitic Chaos.