Circle Inversion Fractals

Inversion Limit Sets

Three Circle Limit Sets

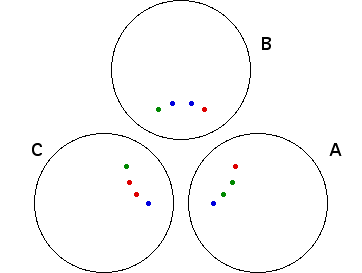
Continuing in the same fashion, the green points in A invert to two points in C and to two points in B.

The red points in C invert to two points in A and to two points in B.

The blue points in B invert to two points in A and to two points in C.

So each circle contains at least 8 limit points.

Of course, we need not stop here. Continuing this process infinitely many steps gives an infinite set of limit points.

The limit points of this set are also limit points of the inversions, and taken together, they form a Cantor set of limit points.

So with just three circles, the limit set can be a fractal.

Return to Three Circle Limit Sets.