Box-Counting Dimension of the Koch Curve

Covering the Koch curve with smaller and smaller boxes we see the pattern illustrated in the table on the right.
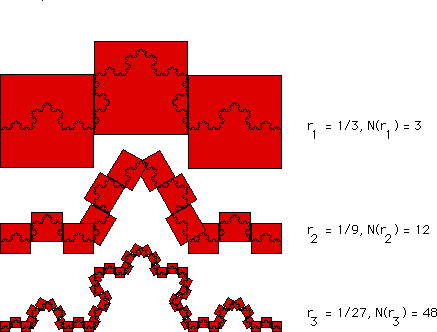
	. N(1/3) = 3 N(1/9) = N((1/3)2) = 12 = 3⋅4 N(1/27) = N((1/3)3) = 48 = 3⋅42 and in general N((1/3)n) = 3⋅4n-1
Here is the Log-Log plot to estimate the box-counting dimension of the Koch curve. In this case, the pattern is simple enough that we can find the exact value of the dimension.

Return to Box-Counting Dimension.