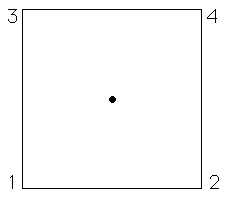
| For example of the Chaos Game, take four vertices, |
| (a3, b3) = (0, 1) |
 |
(a4, b4) = (1, 1) |
| (a1, b1) = (0, 0) |
|
(a2, b2) = (1, 0) |
|
| the corners of the unit square, and take r = 1/2. |
| Suppose the random number generator begins by selecting the
vertices in this order: 1, 3, 4, 3, 2. |
| Click the picture to see the
first five points generated by this run of the chaos game. |
 |
| If we continue, the points will fill in the square. |
| This should be
plausible: we start with a point inside the unit square, and each move is half-way
between where we are and a corner of the square, so we never leave the square. |
| Because we select the corners randomly, no part of the square is preferred over any
other. |
| So since some parts of the square fill in, all parts must fill in. |
| Do you believe this argument? |
| Look at Chaos Game Problems
to test your intuition.
|