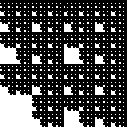| We have observed that any sequence containing a forbidden
sequence is itself forbidden. For example, any triple containing a forbidden
pair is forbidden. |
| On the other hand, a subsequence of a forbidden sequence need
not be forbidden. If ijk is a forbidden triple, we may not assume either
ij or jk is forbidden. |
| We illustrate this with a simple example. On the left
we see the picture resulting if the pair 11 is forbidden; on the right, the picture
if the triple 111 is forbidden. |
|
| By specifying both forbidden pairs and forbidden triples - that is,
equipping IFS with a two-step memory - we can
generate a much wider variety of fractals than with a one-step memory IFS. |
| Here is the software representation of 2-step memory. |
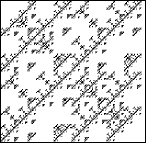
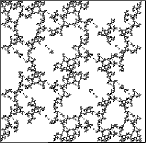
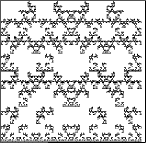
| Here are some fractals generated by
two-step memory IFS. All the pictures are
different, but some of the differences are subtle. |
| Click each picture for an enlargement and the software representation in a new window. |
|
|
There are 264 = 18,446,744,073,709,551,616
different fractals built with two-step memories. With three-step memories,
2256 fractals can be built. This is a
big number. |
| By adding more steps of memory, we can reproduce any figure
to any specified accuracy. Consequently, IFS with memory gives another approach
to using fractals for data compression. An interesting problem is to find the
shortest memory to produce a given shape. This problem is being investigated. |