Addresses in the Koch curve

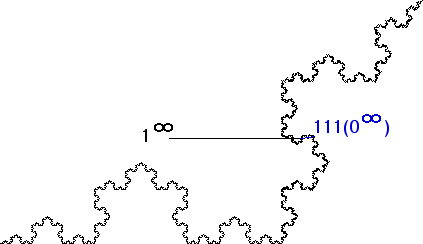
8.(d) Consider the point 1infinity.

To show this point has no tangent, we shall produce a sequence of points converging to this point, with the chords winding round and round 1infinity.

Next, consider the chord between the point 1infinity and the point 111(0infinity).

Now the pattern should be clear: the sequence of points 1k(0infinity) converges to the point 1infinity, and as k increases the chord from 1k(0infinity) to 1infinity winds round and round.

Return to Address questions.