Block Fractals

Background - the Scaling Relation

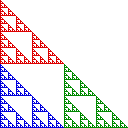
For lines, squares, and cubes we have seen there is a relationship between a scaling factor r and the number N(r) of copies of a similar shape, scaled by a factor of r, needed to cover the original shape.

Representing by d the Euclidean dimension of these shapes, the relationship is

N(r) = (1/r)d.

Now we assert that if this scaling relationship holds for a shape, then the value of d is the dimension of the shape.

Taking the log of both sides of this equation and solving for d we obtain

d = Log(N(r))/Log(1/r).

For example, the Sierpinski gasket (left) is made of N(1/2) = 3 copies scaled by r = 1/2 (right).

So the dimension is Log(3)/Log(2).

Return to Background.